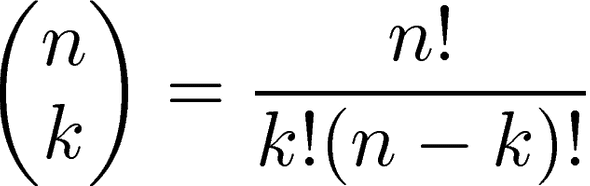NYU Bridge to Tandon - Week 5 part 2
August 05, 2020
Module 7 - Functions
We introduce the k-combinations problem, that is, for some non-negative numbers n and k where n is the size of the collection (number of cards in a deck, number of dishes in a buffet line) and k is the size of the combination and n >= k, we define the number of possible unordered ( aka “red blue green” and “blue green red” are unique) combinations - n choose k - as (n! / (k! * (n-k)!)),
For example, if we have a collection of n = 5 objects and want to know all the number of k = 3 possible combinations, we calculate (5! / (3! * 2!)) or 120 / 12 = 10 possible combinations.
The mathematical notation looks like:
If we wanted to do this with while loops, we can formulate as
int main() {
int n, k;
cout << "enter n and k"
cin >> n >> k
int nFact = 1;
for (int i = 1; i <= n; i++) nFact *= i;
int kFact = 1;
for (int i = 1; i <= k; i++) kFact *= i;
int nkFact = 1;
for (int i = 1; i <= (n-k); i++) nkFact *= i;
cout << "the answer is " << (nFact / (kFact * nkFact);
return 0;
}There’s repeated logic here that distracts us and doesn’t add expressivity in the factorial logic. We now learn how to make our own functions.
We need a function we’ll call factorial that takes an int that represents the number we want the factorial of, and return an int as the answer. So we define a header which looks like
/*
RETURN_TYPE FUNCTION_NAME(ARG_TYPE ARG_NAME, ...) {
FUNCTION BODY
RETURN
}
*/
int factorial (int num) {
int result = 1;
for (int i = 1; i <= num; i++) {
result *= i;
}
return result;
}Using these functions, we can clean up our main function as
int main() {
int n, k;
cout << "enter n and k"
cin >> n >> k
int nFact = factorial(n)
int kFact = factorial(k)
int nkFact = factorial(n - k)
cout << "the answer is " << (nFact / (kFact * nkFact);
return 0;
}Function calls then can be considered their own control flow, by jumping to a position we’ve been in (the function block) and return later.
Using the runtime stack model, we can understand the execution of this function. Our main program will exist in a frame on the stack with all local variables (nFact, kFact, etc). So n=5 and k=3 would get stored in the frame, then the calls to factorial need to be evaluated before nFact can be assigned a value. So we create another frame for factorial with local variables, along with the return address of where we go to when the factorial function is done. Then we associate the arguments of the function with the parameters - that is, factorial(5) should tell the frame that num = 5. During evaluation, the frame only has access to its own variables, it CANNOT access variables in another frame. After evaluation, we pop the frame off the stack and jump back to the return address with the value of the function.
This chapter of Crafting Interpreters is a great but detailed explanation of an implementation.
Note: C++ functions must be declared before usage. So you cannot write the main function at the top of a file and have functions below. Either write in another file and include, or just define it above the main function. We can also just declare the header inline ahead, something like
int factorial(int num); // no body, only header
int main() {
// using factorial
}
int factorial(int num) {
// actual implementation
}Aside: a function that does not return (only does I/O) has a return type of void.
When we pass variables into functions, it is default pass by value (sometimes called call by value). That is, a function that receives variables cannot mutate those variables. It can only act with the values.
If we want to pass parameters into functions, we can also use pass by reference or call by reference with an address-of operator in the function, eg void func(int &x) . So, if we wanted a function that swapped the values of two parameters:
void swap(int &a, int &b) {
int temp = a;
a = b;
b = temp;
}
int main() {
int a = 1;
int b = 2;
swap(a, b);
return 0;
}In this example, the swap stack frame hold references to a and b rather than the values. This means that when swap makes changes, it changes the variables in the main stack frame rather than its local stack frame.
Okay, new program. Take a positive integer num and write the number of digits and sum of digits. We can’t just have one function that returns TWO values (number of digits and sum of digits). So instead we can use call-by-reference to pass in the values and update in the function
void analyzeDigits(int num, int &count, int &sum);
int main() {
int num, count, sum;
cout << "enter a positive integer: ";
cin >> num;
analyzeDigits(num, count, sum);
cout << "the number of digits in " << num << " is ";
cout << count;
cout << " and the sum is ";
cout << sum;
return 0;
}
void analyzeDigits(int num, int &count, int &sum) {
count = 0;
sum = 0;
while (num > 0) {
int digit = num % 10;
num /= 10;
count++;
sum += num;
}
}Problem Solving with C++, Chapter 4
The top-down design or stepwise refinement of a problem it to divide it into smaller and smaller subproblems that become trivial to implement, and then stitch those steps together. In C++, we can separate these subproblems into functions.
C++ has built in libraries with predefined functions that we’ve used before, like sqrt from cmath. A function has arguments attached to parameters and also (often) has a return value. When we use a function, we call or invoke it, such as int root = sqrt(3.0)
When we bring a function into a file, we can add it via include directives a la #include <cmath>. The value in the angled brackets is the name of a file called the header file which dictates the structure of a function - return type, function name, parameter types and names. Header files do NOT include implementation.
Include directives are handled by the preprocessor in a step that looks like copy-pasting the code into the file including the library. You can see what it looks like with clang++ -E FILE_TO_COMPILE
Another function is type casting via static_cast - for example
static_cast<double>(9);We can also declare and define our own functions. Function declaration (or the function prototype) describes how a function is CALLED (the header). Function definition describes what a function DOES. Declarations must happen before a function is invoked, but definition can occur later. In a declaration, we have formal parameters to stand in for the values that a function will actually be called with. Note: formal parameters are optional but types are mandatory, yet we will use parameter names for clarity.
When a function is invoked, by default we plug in values for the parameters in a call by value mechanism (see above notes).
Arguments are invoked by order! Cannot mix and match the order between declaration and invocation.
We use functions as black boxes to hide information about implementation. A programmer may need to know what a function does without how it does it. Implementation may change but function APIs may not - think about a more efficient search algorithm. Writing and using functions as if they were black boxes is also called procedural abstraction.
When variables are declared inside a function they are locally scoped and do not leak outside. For a value that is needed by many functions, we might use a globally scoped constant by defined it outside all functions.
Technically, everything exists in some block scope where blocks are defined within curly braces, and global scope is the global block.
Note: Our using directives can be block scoped as well if we want to open a namespace locally to a function. This can help avoid clobbering.
C++ offers function overloading where we can define functions with different arity or parameter types and the same function name. We’ve seen examples with the division operator that can work on doubles, floats and ints in different ways. For example:
int add(int a, int b);
int add(int a, int b, int c);
double add(double a, double b);When you overload a function name, the function declarations for the two different definitions must differ in their formal parameters. You cannot overload a function name by giving two definitions that differ only in the type of the value returned.
Problem Solving with C++, Chapter 5
Functions can return void. For void functions, we can omit the final return. This is useful for I/O like writing to terminal, or call by reference mutation. Defining a function that calls by reference just adds an ampersand before the reference variable, eg void example(int &x).
Since program variables are implemented as memory locations, a reference is actually a variable whose value is the memory location. This allows us to circumvent scope limitations. We are also allowed to mix call-by-value and call-by-reference in function parameters.
When we write function declarations, we can add comment blocks to describe preconditions (what we assume to be true) and postconditions (the effect of the function).
We can write driver programs to test our functions. These a small, temporary tools (often loops) to test various inputs
int main() {
do {
functionStuff()
} while (inputIsValidRunner)
}We can also add stubs that just replace a function dependency with an output value so we don’t test more than the one function we care about. Example:
// stub
int taxableIncome(int salary) {
return 100;
}
int totalSavings(int salary) {
// our function we want to test
}
int main() {
int income = taxableIncome();
return totalSavings(income);
}We can use the assert macro with a boolean expression as a precondition
#include <cassert>
int function() {
assert(booleanExpression);
// do stuff
}To disable assertions, add #define NDEBUG above the include directive.
Data structures and Algorithms in C++, Chapter 2
We’re now into algorithm stuff. Some rules:
Definition 2.1: T(N) = O(f(N)) if there are positive constants c and n0 such that T(N) ≤ cf(N) when N ≥ n0. My note - this is the upper bound
Definition 2.2: T(N) = Ω(g(N)) if there are positive constants c and n0 such that T(N) ≥ cg(N) when N ≥ n0. My note - omega is the lower bound
Definition 2.3: T(N) = θ(h(N)) if and only if T(N) = O(h(N)) and T(N) = Ω(h(N)). - Theta is the actual value, so time is equal to lower bound and upper bound
Definition 2.4: T(N) = o(p(N)) if, for all positive constants c, there exists an n0 such that T(N) < cp(N) when N > n0. Less formally, T(N) = o(p(N)) if T(N) = O(p(N)) and T(N)=/= θ(p(N)). 51
We are concerned with relative rates of growth that help us determine which functions take more time than others. We throw away constants and note that this is about eventuality so: 1000N vs N^2 - N^2 for some value of N will eventually overtake 1000N, thus we say that N^2 is the limiting factor.
We call the first definition Big-O notation.
We ignore constants and lower order - eg we don’t write O(N^2 + N) becaues N^2 is the dominant element.
Note: These are algorithmic analyses. We cannot, in the real world, ignore caching, memory locality, disk I/O time, etc. However, we do work with massively large numbers of inputs in programming so these analyses become useful tools.
Rules
- For loops - the running time is at most the number of elements of the loop
- Nested loops - analyze inside out. The running time is the inner loop’s runtime multiplied by the number of times it is executed, the number of elements in the outside loop
- Consecutive work - it’s additive. So two sequential for loops become O(N) + O(N) = O(2N), and we throw away constants so it’s O(N)
- If/else - the running time is never more than the running time of the condition plus the larger of the work in the if/else branches
Logarithmic algorithms might be confusing but it is defined as:
O(logn) if it is constant time to cut the problem size by a fraction (like divide and conquer algorithms like binary search)
Module 8 – Algorithm Analysis
We’ll look at the problem of seeing if a number is prime or not, and learn how to talk about runtime complexity.
bool isPrime (int num) {
// count the number of integers that divides cleanly into num
// aka, num % i == 0
// only correct answer is 1 and num for a prime
int countDivs;
for (int i = 1; i <= num; i++) {
if (num % i == 0) countDivs++;
}
return countDivs == 2;
}We know we can cut the problem space in half: let k be some int between num/2 and num - there is no complementary divider that is an integer. That is, d = num / k and if k > num/2 then d < 2
bool isPrime (int num) {
// count the number of integers that divides cleanly into num
// aka, num % i == 0
// make sure only number in first half is 1
int countDivs;
for (int i = 1; i <= num/2; i++) {
if (num % i == 0) countDivs++;
}
return countDivs == 1;
}There’s a third version! Instead we can look up to sqrt(num). Think about 100 - the largest unique divisor is up to sqrt(100) = 10. 20 divides into 100, but 5 times which we checked up to sqrt. That is, every number after the sqrt has a complementary divider LESS than sqrt.
Proof by contradiction: let k and d be complementary dividers of num (k * d == num). Assume BOTH are greaterr than sqrt(num). we can then say k * d > sqrt(num) * sqrt(num) or num > num. Contradiction, implying that both k and d cannot be greater than sqrt. Thus at least one must be greater.
#include <cmath>
bool isPrime (int num) {
// count the number of integers that divides cleanly into num
// aka, num % i == 0
// make sure only number in first half is 1
int countDivs;
for (int i = 1; i <= sqrt(num); i++) {
if (num % i == 0) countDivs++;
}
return countDivs == 1;
}Runtime analysis:
Time 1 (T1), Time 2 (T2), Time 3 (T3). We know the running time depends on the size of the integer. Let n be the size of the input. Let us parameterize the running time over the size of the input. Running time depends on operators, so we ignore machine-dependent constants and count all primitive operators (addition, multiplication) as 1. We also only care about asymptotic analysis - we care about asymptotic order of the input. So drop lower order terms and constants.
T1(n): O(n) = O(n)
T2: O(n/2) = O(n)
T3: O(sqrt(n))
Formal definition
Asssume two functions f(n) and g(n) mapping positive integers to positive g(n)
We say f(n) = O(g(n)) if there exists to real constants c1 and c2 and a positive integer n0 such that c2 * g(n) <= f(n) <= c1 * g(n) for all n >= n0.
Proof: 3n^2 + 6n - 15 = O(n^2)
Find upper bound:
Drop leading constants
3n^2 + 6n - 15 <= 3n^2 + 6n
Find an upper bound by adding a 6n
3n^2 + 6n - 15 <= 3n^2 + 6n <= 3n^2 + 6n^2 = 9n^2
we can then say c1 = 9
find lower bound:
3n^2 <= 3n^2 + 6n - 15 <= 3n^2 + 6n <= 3n^2 + 6n^2 = 9n^2
if 3n^2 <= 3n^2 + 6n - 15
then 6n - 15 >= 0
n >= 2.5
Then we can say n0 = 3
Then we can drop lower order constant 6n
3n^2 <= 3n^2 + 6n - 15 <= 9n^2
Then we can say c2 = 3
Therefore 3n^2 + 6n - 15 = O(n^2)
Discrete Math Section 5.1
How do we count combinations of numbers? We have two rules we’ll start with.
Product rule - The product rule says that for N number of sets, the cardinality of the Cartesian product is the product of the cardinality of each set. That is, |A1 x A2 x .. x An| = |A1| * |A2 * … * |An|. For example, if we wanted to know all combination of breakfasts given:
main: {eggs, pancakes, waffles}
sides: {toast, bacon}
drinks: {coffee, water, orange juice}
The cardinality of set of all combinations is 3 * 2 * 3 = 18
This works for strings too - for example, If Σ is a set of characters (called an alphabet) then Σ^n is the set of all strings of length n whose characters come from the set Σ. For binary, for binary strings of length 5, we know there are 2^5 = 32 possible combinations.
Sum rule - The sum rule says that, for N number of sets, if they are mutually disjoint then the union of |A1 u A2 u … u An| = |A1| + |A2| + .. + |An|
That is, if you know all options and only pick one element from the sets, then the number of options is equal to the sum of the cardinalities. Given our above menu of mains, sides and drinks, and user can only pick one, the sum rule states that the number of options is 8.
The book uses passwords as an example to merge these two.
Assume that L is the letters of an alphabet (all lower case) and D are the digits. |L| = 26, |D| = 10. The set of all characters is C = L union D, so the size of the set C is |C| = |L| + |D| = 36. Assume we must have passwords between 6 and 8 characters. The sum rule, since each letter combination is disjoint, says |C6 union C7 union C8| = |C6| + |C7| + |C8|. For each, we can apply the product rule and get 36^6 + 36^7 + 36^8.
Discrete Math Section 5.2
The bijection rule says that if there is a bijection from one set to another then the two sets have the same cardinality. This allows us to take a set of unknown cardinality, find a bijection to a set of known (or easily counted) quantity, then assert the count of the first set.
For example, if you have a movie theater and want to count the number of people who attended in a day, you can define a bijection as the number of tickets at the end of the day. You then have a well defined inverse.
We can also use this to count the number of elements in a power set of a finite set X. If |X| = n, then we can say that f is a bijection:|{0, 1} ^n| = |P(x)| where a bit being 0 is the absense of an element in the set and 1 is the presence.
The k-to-1 correspondence defines a relationship of K elements in set X for every element in set Y - that is, if each guest has two shoes then the number of shoes should be 2x the number of guests, thus k = 2.
Formally - Let X and Y be finite sets. The function f:X→Y is a k-to-1 correspondence if for every y ∈ Y, there are exactly k different x ∈ X such that f(x) = y.
Discrete Math Section 5.3
The generalized product rule says that in selecting an item from a set, if the number of choices at each step does not depend on previous choices made, then the number of items in the set is the product of the number of choices in each step.
An example - I go to the same restaurant every day for lunch. They have 10 lunch specials. I want to try something new every day this work week. On Monday I have 10 options. On Tuesday I must eliminate yesterday’s choice, giving me 9 options. On Wednesday I lose another. The number of total combinations is 10 * 9 * 8 * 7 * 6.
Discrete Math Section 5.4
Building off the generalized product rule, an r-permutation is a sequence of r items with no repetitions, all taken from the same set. In this case, order does matter so the sequences ()“red”, “blue”, “green”) and (“blue”, “green”, “red”) are different permutations.
The number of r-permutations in a set of length n where r <= n, called P(n, r), is n! / (n-r)!
That is, if n = 5 and r = 3 then (5 * 4 * 3 * 2 * 1) / (2 * 1) = 5 * 4 * 3
A permutation (without the parameter r) is a sequence that contains each element of a finite set exactly once. You can think of it as an r-permutation where r = the number of elements in the set. The number of options is n! (n-factorial)
Example - imagine I have 4 people at a dinner party (Alice, Bob, Carol, Dan). I want to seat them at a bench, but I want Carol and Dan to sit next to each other. How many options do I have?
First, Carol and Dan - I have two options to sit them next to each other (Carol then Dan, or Dan then Carol). Then I need to figure out the number of ways to seat Alice, Bob and the Carol/Dan pair. That’s 3! (three discrete elements) times 2 for the number of ways I can organize the pair, for 12 options.
Question: A wedding party consisting of a bride, a groom, two bridesmaids, and two groomsmen line up for a photo. How many ways are there for the wedding party to line up so that the bride is next to the groom?
Answer: 240. First decide whether the bride is to the left or right of the groom (2 choices). Then glue the bride and groom together and there are 5! ways to permute the five items. By the product rule, the number of line-ups with the bride next to the groom is:
Discrete Math Section 5.5
An r-combination, sometimes called an r-subset, is a way of counting order-independent combinations of elements from a set. If you care about which three people from an election got the most votes and win representative seats, order doesn’t matter so {Alice, Bob, Carol} and {Carol, Bob, Alice} are the same - note the set notation.
To calculate the number of r-combinations in a set, you start with the number of permutations and divide by r!.
The notation is the same as the above n-choose-k example, but we can also say C(n, r) for n-choose-r
That is
- P(n, r) / r!
- n! / ((n-r)! * r!)
An equation is called an identity if the equation holds for all values for which the expressions in the equation are well defined. We can say C(n, r) = C(n, n - r) is an identity because it holds true for all non-negative n and any r from 0 to n.
Discrete Math Section 5.6
One of the examples here specifies words / phrases to look for that hint at combinations vs permutations. For example, given 10 people and 4 prizes, how many ways can you allocate them if
- the prizes are all the same? Order doesn’t matter so it’s combination, C(n, r) or (10! / (6! * 4!))
- The prizes are all different? Order does matter, so it’s permutation, or P(n, r) or 10! / 6!
Review book for more examples of non-mathematical terms. eg if a waiter puts dishes in the center of a table, the number of ways to order from the menu is the combination (subsets) - if everyone gets a dish it becomes permutations (order counts).
Discrete Math Section 5.7
Counting by complement is a strategy of counting the number of elements in a set S that have some property P by removing the elements that do not have P. That is
|P| = |S| - |P’|
Discrete Math Section 5.8
A permutation with repetition is an ordering of a set of items in which some of the items may be identical to each other. That is, how do you find the r-permutation of something that has repeats, like the string “MISSISSIPPI”?
In order to do so, you need to find the r-subsets for EACH repeated element where N is the number of remaining spots and R is the count of that element, then use the product rule to determine the answer.
Mississippi has 4 s, 2 p, 3 i, 1 m - we can then do 11-choose-4 * 7-choose-2 * 4-choose-3 * 1-choose-1.
There’s an easier way!
The formula is defined as n! / (n1! * n2! * n3! … nk!) where k is the number of elements, and nk is the count of element k.
So for Mississippi it becomes 11! / (4! * 2! * 3! * 1!)
I work and live in Brooklyn, NY building software.