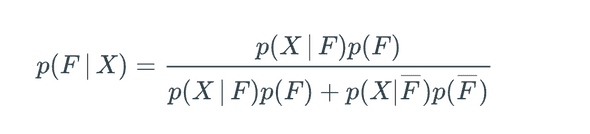NYU Bridge to Tandon - Week 5 part 2

Module 9 - Arrays

The basic properties of arrays

1. Arrays are stored continuously in memory (one uninterrupted section)
2. Elements are all of the same type
3. We access elements via 0-based index

The compiler uses the index as an offset, so the math is

addressOfElementAtIdxI = addressOfStart + i * sizeOfEachElement

This downsize of this math is that we can access arbitrary memory by passing any index in - if i is out of bounds, it’ll basically say “go to the start of the array, go to i * size and get what’s there” EVEN if i is not in the array. Security flaw in business logic.

These arrays are technically static arrays (we’ll cover dynamic arrays later) - static arrays are stack allocated. As a result

Array size MUST be a compile-time constant and given at declaration

So how would we calculate the average of a list of grades AND the number of grades above the average?

#include <iostream>
using namespace std;

const int MAX_SIZE = 60;
int main() {
	int numberOfStudents;
	cout << "Enter the number of students in the grade (max " << MAX_SIZE << "): ";

	cin >> numberOfStudents;

	if (numberOfStudents > MAX_SIZE) {
		//error
	}

	int grades[MAX_SIZE];
	int sum;

	for (int i = 0; i < numberOfStudents; i++) {
		int grade;
		cin >> grade;
		sum += grade;
		grades[i] = grade;
	}

	double average = (double)sum / numberOfStudents;
	cout << "the class average is " << average;
	cout << " and the grades above that are ";

	for (auto grade: grades) {
		if (grade > average) {
			cout << grade << " ";
		}
	}

	return 0;
}

Problem Solving with C++, 7.1

An array provides an interface over a finite collection, or list of elements that are all of the same type T. For example, if we want to see a list of all the receipts I have from Ample Hills (oh no), we might declare float receipts[12];

Our syntax declares the TYPE of the element, the name of the collection, and the size of the array. Arrays are fixed size in C / C++ due to stack allocation, and needing the size to be known at compile time.

We can access variables by their index, or position by order, starting from 0 as the first element. That is, the first expense I have at Ample Hills would be receipts[0] and the last receipts[11]

We can declare arrays alongsize other variables with something like int height, sandwiches[5], weight. Array index accessors also allow us to write to an array, which looks like sandwiches[5] = 100;

We can read and write from arrays if we know the length ahead of time. That might look like

const int NUMBER_OF_ICE_CREAM_FLAVORS = 10;
float iceCreamCosts[NUMBER_OF_ICE_CREAM_FLAVORS];

for (int i = 0; i < NUMBER_OF_ICE_CREAM_FLAVORS; i++) {
	cout << "The ice cream at " << i << " is $" << iceCreamCosts[i];
}

How does array access really work?

Imagine the following declaration

int arrayThing[5];

This tells the C++ compiler “reserve space in memory large enough for 5 integers and tell me where the first element is is memory”. That is, the array value is really a memory address; a location in memory where the array starts. Thus, saying arrayThing[0] is the same as “to go the location at arrayThing and tell me what’s there”. But how does arrayThing[3] work? This is the same as telling the compiler “Go to the location of arrayThing, find out how many bytes is the size of 3 of the base type int, then add that value”

That is, if arrayThing is located at 100, and an int is 4 bytes large, this tells the compiler “Go to 100 + 3 * 4 and get me that value”.

Out of range accessing values is illegal and can return garbage values, or allow bug exploitation.

In order to be safe, if we ask a user to tell us where in the array their element is we must validated, to avoid giving them access to arbitrary memory.

We can declare arrays with size and elements by using braces and commas like int children[3] = {2, 12, 1}

C++ introduces a range based for loop with

for (int child: children) {
	cout << child;
}

That is, we declare the data type and the name of the variable to identify the element in the array. Note that the variable is pass-by-value - you cannot change the array. You CAN declare it with a pass-by-reference style such as

for (int &child: children) {
	cout << child;
}

C++ also allows the auto keyword to infer type.

for (auto child: children) {
	cout << child;
}

Problem Solving with C++, 7.2

Sending an array-index-accessor into a function is valid. That is

bool isOne(int num) {
	return num == 1;
}

int arr[5] = {1, 2, 3, 4, 5};

isOne(arr[0]);

Is syntactically correct. The index accessor will be evaluated prior to function call.

We can also pass in entire arrays as a function argument. They end up behaving similar to pass-by-reference (that is, functions can write to them)

A function parameter can be an array of some type T, and the function can also take array size for iteration

void writeToArray(int arr[], int size) {
	for (int i = 0; i < size; i++) {
		arr[i] = 100;
	}
}

Due to the way arrays are stored in memory, you need to tell a function how many elements are in the array. Specifically, when you pass an array into a function technically all you’re doing is telling the function where in memory the array starts, and how large each element is in bytes. You don’t pass the third piece of array-information, the size. So you must do that explicitly.

Since functions can modify arrays passed as arguments, we might want to prevent the code from doing so for compiler-level safety. To do that, we use the const keyword to declare a constant array parameter. That might look like

void readArray(const int arr[], int size) {
	for (int i = 0; i < size; i++) std::cout << arr[i];
}

readArray(someArray, 10);

Problem Solving with C++, 7.3

Sometimes we don’t know at compile time exactly how much memory we need. So we allocate a massive space, one that would cover more than the use case. In this case, we end up with partially filled arrays. When this happens, the unused space (that is, the end range that we don’t populate, the excess) is garbage. We must be careful to NOT access that, by tracking and only using the real value that the user put in.

Module 10 - Strings

C++ has its own string type, which we can use with the directive #include <string>. Strings are double quoted and respond to concatenation with the plus operator. We can read strings with std::cin and write to stdout with std::cout. cin by default only reads up to a space, so keep that in mind.

If we want to capture an entire line, we use

int main() {
	string str;
	cout << "enter your name: ";
	getline(cin, str);
	cout << "Your name is: " << str;
	return 0;
}

Strings can be read with index-accessors like arrays. A string is effectively a sequence of characters, so each element is a char.

We can also slice (find substrings) with a start (inclusive) and length.

str.substr(startIdx, len);

Strings also have a length method on the class, such as str.length()

How can we print a string backwards?

#include <iostream>
#include <string>
using namespace std;

int main() {
	string str;
	cout << "Enter your name: ";
	getline(cin, str);
	int len = str.length();

	for (int i = len-1; i >= 0; i--) {
		cout << str[i];
	}
	return 0;
}

Strings have lexicographic order based on ASCII code from index 0 to length. That is

// pseudocode

for i in min(str1.len, str2.len)
	if str1[i] < str2[i]
		return str1 is less
	else if str1[i] > str2[i]
		return str2 is less
	else
		continue loop

if not yet returns
	shorter string is less, return that

Strings also have a find method to see if the substring of a string exists and where the starting index is (first appearance, in case of duplicates).

	string test = "bananananna"
	int startingIndex = test.find("anna");
	bool notFound = test.find("notInside") == string::npos;

Find can also take an optional starting index as the second param, which will start looking AFTER the second param such as str.find(sample, idxToStart);

Problem Solving with C++, 8.2

Strings are arrays of characters terminated with the null byte '\0'. We include strings via the string directive, which is in the std library so we’ll need to add the namespace std, or access via std::string

We can read all input from a user into a string with the getline function, which stops reading when it hits a newline '\n' We can change that to read until some OTHER character, such as getline(std::cin, stringVar, '?')

String accessors can be protected at runtime with str.at(idx) which throws a runtime error rather than reading garbage values with bracket notation. It also allows you to write with str.at(idx) = 'a';

Discrete Math, 6.1

Language:

Experiment - a procedure that results in one out of a number of possible outcomes

The set of all outcomes is the sample space.

A subset of the sample space is an event.

That is, an experiment could be flipping two coins. The set of opttions, the sample space, is {HH, HT, TH, TT}. The event of at least one head is {HH, HT, TH}.

Discrete probability is concerned with experiments where the sample space is countably finite or countability infinite. What does the latter mean?

A set is countably infinite if there’s a one-to-one correspondence between the elements of the sets and the integers. That is, it’s possible to assign every element in a set to an integer and eventually reach some value by counting, no matter how long it takes. Think about binary strings. We can assign 0=0, 1=1=, 10=2, 11=3, … so on and so forth and, as long as we progress in the set, can reach some integer N.

Probability is concerned with likelihood. Every event has a probability, and the sum of all event probabilities is 1.

A uniform distribution occurs when the probability of every outcome is equal (a dice roll, for example). In a uniform distribution, if every outcome is equally weighted, then the probability of an event is the number of outcomes in the event divided by the total number of events in the sample space.

That is, the probably of 2 or lower when rolling a die is

|{1, 2}| / |{1, 2, 3, 4, 5, 6}| = 2/6 = 1/3

6.1.1

b) {hhtt, thht, tthh} = 3 outcomes / 16 sample = 3/16

c) {thhh, thht, tthh} = 3 outcomes = 3/16

6.1.2

b) There are n! total ways to order the group. If Ceiia is first and Felicia is last, there are (n-2)! possible middle-orderings. Thus, 1 / (n(n-1))

6.1.3

a) There are 2n total socks. We need to choose two. thus 2n choose 2, or n(2n - 1)

b) The ways to pick 2 white socks is n choose 2. The ways to pick 2 black socks is n choose 2. Thus 2(n choose 2) or n (n-1)

c) The total number of ways to pick socks is n(2n -1). The ways to pick matching pairs is n(n-1). Thus, the probability of matching pairs is (n-1) / (2n-1)

Discrete Math, 6.2

If two events have no overlap, we call them mutually disjoint. That is, with two coin flips, the events where we have exactly one head and exactly two heads. Then we can add these probabilities to find the probability of at least one head over two coin flips. This ONLY works when the intersection of events is zero. That is

The probability of exactly one head over two coin flips is .5 {TH, HT}. The probability of exactly two heads is .25 {HH}. The sum is .75

We can formalize as

P(E1 or E2) = P(E1) + P(E2)

If two events are NOT mutually exclusive we can use the Inclusion-Exclusion principle as

P(E1 or E2) = P(E1) + P(E2) - P(E1 and E2)

(this is the same as the above, except in a mutually disjoint case, P(E1 and E2) = 0)

Often times, we can use the complement of an event to determine our probability - that is, it’s easier to reason about the probability an event DOESN’T happen. Then we can calculate

P(E’) = 1 - P(E)

6.2.1

a) Probability at least n-1 heads in n coin flips? Same as odds of no tails + odds of exactly one tails. Odds of no tails = 1/(2^N) and odds of exactly one tails = n / (2^n) -> sum = (n+1) / (2^n)

b) Odds at least two consecutive coin flips are the same? What are odds no consecutive coin flips are the same? 2 / 2^n (HTHTHTH… or THTHTH…). So complement is 1 - (2 / 2^n)

6.2.2

b) Prob of Celia first = 1/n. Prob of Felicity last = 1/n. Prob of Celia first AND Felicity last = (n-2)! / n! = 1 / n(n-1). Make Celia and Felicity n-1 / n(n-1), sum to 2(n-1)/n(n-1) - 1 = 2n-3 / n(n-1)

Discrete Match, 6.3

Sometimes we want to discuss the probability of a thing happening predicated on another event. That is, two coin flips - what are the odds of 2 heads? 1/4. What are the odds of 2 heads, given we flipped one coin and got heads already? 1/2.

We use conditional probability to denote the probability of event F happening given some event E happening, that is p(E|F) - or given E, F.

The formula is

p(E |F) = p(E and F) / p(F)

Which can be simplified to

|E and F| / |F|

For our coin flips, the event E = two coin flips are {HH}. F = first coin is heads. |E and F| = 1 ({HH}. |F| = 2 {HH, HF}. Therefore, 1/2

Another example, let E and F = two dice rolls, the first is 5 and the sum is at least 11. F = event that the first die is 5.

|F| = all the possible two-die rolls where the first is 5. That is, (5,1), (5,2)… = |F| = 6

|E and F| = all the possible ways to sum to 11 or higher, given one die is 5 => 1

1/6

Essentially, we are narrowing down probabilities given some event F happening. Like…the probability I get 100 on an exam AND get accepted into a masters / probability I get 100 on an exam

Two events are independent if conditioning on one event does not change the probability of the other. Think about two dice rolls. Probabiliy both are the same? 6/36 = 1/6. Probability both are same, given first is 5? Well if first is 5 the second must be 5 -> 1, 1/6. These rolls are independent events. Specifically, the odds of the die rolling a 5 on the first roll does not impact the odds of a 5 on the second roll.

If two events are independent then the probabiliy of both happening is the product of the probabiliyt of each happening.

p(X and Y) = p(X) * p(Y)

If EVERY event in a set are indepedent from each other, we say they are mutually independent and calculate

p(A1 and A2 and … and An) = p(A1) * p(A2) * … * p(An)

6.3.1

a)

p(A) = 1/2

p(B) = {46, 55, 56, 64, 65, 66} = 6/36 = 1/6

p(C) = 1/6

b) |A and C| = |{55, 53, 31}| = 3. |C| = 6. 3/6 = 1/2

c) |B and C| = |{55, 56}| = 2. |C| = 6. 2/6 = 1/3.

d) |A and B| = |{46, 55, 64, 66}|. |B| = |{46, 55, 56, 64, 65, 66}|. 4/6 = 2/3

6.3.3

a) There are 8! total ways to line up the party. To have bride and groom next to each other, we have 7! total variations, times 2 for bride before groom or vice versa. = 2 / 8 = 1/4

b) There are 7! ways to arrange a group with MoH on the left. There are 8! total arrangements. 1/8

c) p(A) * p(B) = 1/32. P(A and B) = 2 * 6! total arrangements of MoH on left and BG together / 8! total. 2 / (8 * 7) = 1 / 28. Not independent.

6.3.5

Total number of hands is 52 choose 5.

A - Total number of ways to pick a 4-of-a-kind is equal to (13 choose 1) * 48 - picking one rank and 1 of the leftover cards.

B - Ways to pick from no aces = 48 choose 5, at least one ace = 1 - 48 choose 5.

Discrete Math, 6.4

Bayes’ Theorem is a way of reasoning about probability based on the evidence of outcomes.

Specifically, Bayes’s theorem lets us theorize about p(F | X) if we know p(X | F), p(X | F’), and p(F).

Assuming F = a fair die is selected, and F’ = an unfair die loaded with 2/7 probability of rolling a 6, and X = a die rolls 6.

What is the probability of selected a fair die and rolling a 6 given rolling a 6?

Well, if we know the probability of rolling a 6 and selecting a fair die given a fair die (1/6), the probability of rolling a 6 and selecting an unfair die given an unfair die (2/7), and the probability of a fair die (1/2).

we can calculate

the numerator = 1/6 * 1/2 = 1/12

The denominator = 1/12 + (2/7) * (1/2)

The probability then = ~0.37

5/72 / (5/72 + 10/98) = 49/121

6.4.1

a)

Let F = biased coin

p(B) = 1/2. P(X | B) = (3/4)^7 * (1/4) ^ 3.. P(X | B’) = (1/2) ^ 10

( ((3/4)^7 * (1/4) ^ 3) * 1/2) / ((3/4)^7 * (1/4) ^ 3 * 1/2) + 1/2 * (1/2) ^ 10)

0.00104 / (0.00104 + 0.00048)

0.6842

6.4.2

Let F = fair die

p(F) = 1/2

p(X | F) = (1/6)^6

p(X | F’) = 0.25^2 * 0.15^4

(1/6)^6 * 1/2 / ((1/6)^6 * 1/2 + 0.25^2 * 0.15^4 * 1/2)

0.4038

Discrete Math, 6.5

A random variable X is a function from the sample space S to an experiment of real numbers, where X(S) is the range of the function X.

If two dice are rolled, the random variable D is the sum of the rolls, so D(x, y) = x + y

If X is a random variable and r is a real number, then X = r is an event. That is, for rolling two dice, if D(x+y) = 5, then that’s an event with the subset of {(1, 4), (3, 2), (4, 1)}

The distribution of a random variable is the set of all pairs (r, p(X = r)) for all r in X(S)

6.5.1

a) {1, 2, 3, 4, 5, 6, 4, 8, 10, 12, 9, 15, 18, 16, 20, 24, 25, 30, 36}

b) 4 / 36 = 1/9

Discrete Math, 6.6

The expected value of a random variable is defined as

E[X] = the sum of all X(s) * p(x) for all s in the sample space.

That is, the expectation of a random variable is equal to the sum of all elements in the range * the probability we will see them.

If X = winning 100000000 dollars in the lottery, and only one ticket can win, and the number of possible tickets are 50^6

then E[X] = 100000000 * (1 / 50^6) + 0 * (1 - 1 / 50^6) = ~0.0064

This can also be calculated as

E[X}] = r * p(X = r) for all r in X(S).

6.6.1

Let |S| = 10 choose 2 = 45

Number of ways to pick two girls = 7 choose 2 = 21

Number of ways to pick 1 girl = 7 choose 1 * 3 choose 1 = 21

E[G] = 2 * (21/45) + 1 * (21/45) = 63/45 = 21/15 = 7/5

6.6.2

E[D] = 2 * 1/6 + 1 * 1/6 + -1 * 4/6 = -0.17

Discrete Math, 6.7

Linearity of expectations says the expectation of the sum of two random variables is equal to the sum of the expectations.

If X and Y are two random variables in S, and c is some real number constant

E[X + Y] = E[X] + E[Y]

E[cX] = cE[X]

From the book

Two friends run a lemonade stand over the summer. It takes 10 lemons to make a batch of lemonade. Usually, lemons are 50 cents apiece, but with probability 1/4, they are on sale for 40 cents apiece. If there is a baseball game at the park where they put up their stand, they will sell $20 worth of lemonade. If there is no baseball game, they will sell $10 worth of lemonade. On a given day, there is a baseball game with probability 1/2. What is the expected profit?

E[P] is the same as E[R - C] where R is revenue and C is cost

E[R - C] = E[R] - E[C]

E[R] = 0.5 * 20 + 0.5 * 10 = 15

E[C] = 3/4 * 5 + 1/4 * 4 = 4.75

15 - 4.75 = 10.25

Discrete Math, 6.8

A Bernoulli trial is an experiment wiht two outcomes - success and failure.

In a sequence of trials, called a Bernoulli process, the outcomes of the experiments are assumed to be mutually independent and have the same probability of success and failure. Success denoted by p and failure as 1-p

The probability of exactly k successes in a sequence of n independent Bernoulli trials, with probability of success p and probability of failure q = 1 - p is

The distribution over the random variable defined by the number of successes in a sequence of independent Bernoulli trials is called the binomial distribution. The probability that the number of successes is k in a sequence of length n with probability of success p is denoted by b(k; n, p).